特異点のなかでも特異的な真性特異点

　ブログ名からして複素関数論での「特異点」に触れないわけにはいかない。
そんな見当違いな使命感から、特異点の事例を見える化してみます。

　Ｅｘｐ（１／ｚ）の名だたる特異点はｚ＝０です。ローラン展開すればわかるように、

　この級数から、ｚ→０にて無際限にｚが発散しまくるのは、なんとはなしに理解できましょう。これを「真性特異点」と称します。

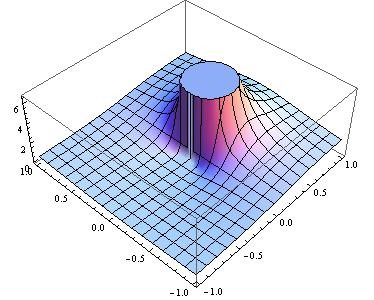
実際、Ｅｘｐ（１／ｚ）の絶対値がどうなるのかは、下図です。|z|<１です。

　関数の絶対値が、ｚ→０にて無限にでかくなるのはいいとして、真性の真性たるわけは偏角を見える化すると理解が行き届くでしょう。

絶対値の図とは異なる特性が出てきていますね。
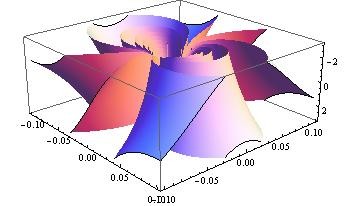
もっとｚ＝０近傍を拡大してみます。

　関数値の偏角は大きな袋とじが何重にも合わさって、原点を包み込んでいるようです。偏角が多値化しているということは、同じ絶対値で複数の関数値が何度か重複発生していることを示唆します。
　これがピカールの大定理の一例となってくるわけでしょう。

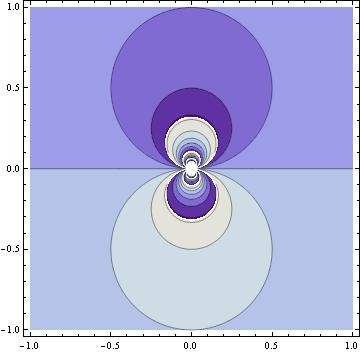
上からこの偏角の模様を覗き込むとこんな感じです。虚軸上に２つの同心円構造があるのです。

$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
【参考書目】
やはり関数の理解には視覚化でございますな。とりわけ複素関数論は面白みのあるイメージが
理解を促進するような気がします。

ヴィジュアル複素解析